by Peter Farey

In William Shakespeare: A Textual Companion, which partners the Oxford Complete Works, Gary Taylor made use, amongst other approaches, of the relative frequency of various 'function words' to determine how far one could be confident that various works either were or were not within the Shakespeare canon. He said that authors tend to have a typical pattern in the frequency with which they use various common words. The words he chose, because of what he said was the relative consistency of their use within the known Shakespeare canon, were: but, by, for, no, not, so, that, the, to and with.

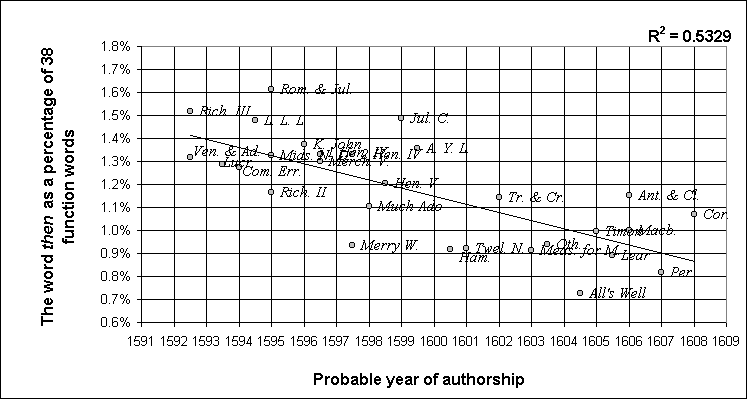
Surprisingly, Taylor did not use this approach in considering the chronology of the plays: surprising, since the frequency of the use of such words does sometimes show a marked increase or decrease over the course of Shakespeare's career. Taylor's 10 function words had been from an original list of 38, some of which do change quite significantly. Figure 1, for example, gives the relative frequency of the word then (shown as a percentage of all 38 words). This is plotted against the year in which, according to Taylor, each of the works seems most likely to have been written. For the purposes of this exercise we shall be more interested in the data up to about 1609, so the graph is cut off at that date. Works thought to be from 1592 or earlier have also been excluded. A line of best fit (least squares) is shown, with the coefficient of determination (R²) indicating the extent to which the variation about the mean is 'explained' by the trend, in other words the trend's validity.

Figure 1

Then gives the highest R² value of the 38 function words, as is shown below.

A graph similar to Figure 1, but this time dividing a group of the 'increasing' words by a group of the 'decreasing' ones, is shown as Figure 2.

Figure 2

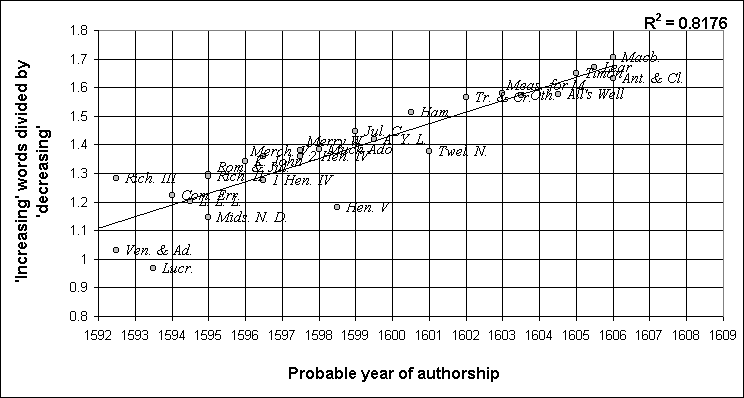
The words used were all of those with R² values of more than .05. Given that six of Taylor's ten words are thus included, one cannot but wonder about his definition of 'consistent'. The overall R² value of .8176 reflects the high validity of the trend, as is clearly discernible.

The purpose of this paper is to see whether, having observed such a trend, we can use it to gain an indication of the order in which The Sonnets were written. Was the original order, as printed by Thomas Thorpe, more or less that in which Shakespeare wrote them, or are the many authors and editors who have attempted to find a 'better' sequence on the right track?

Clearly, the individual sonnet is far too small an entity to be dated in this way. Dealing with groups of sonnets, however, we may be able to find patterns emerging. We do nevertheless need to count how many of the 22 function words appears in each of the 154 sonnets. The result is fairly emphatic. Looking first of all at whether in the case of each sonnet there are more 'decreasing' words or more 'increasing', we obtain the following picture:

This yields a chi-squared value of 12.07, which is highly significant at the p = .001 level, and therefore lends considerable support to Thorpe's original sequence having reflected the order in which they were written. The 'missing' 20 Sonnets are those with the same number of each type of word.

Next we can consider it simply in terms of how often the two types of word appear overall in either the first half or the second half of the collection.

This time the chi-squared value is even greater, coming out at 17.73, which is again highly significant at the p = .001 level.

We can see the first of these tables illustrated quite clearly in Figure 3, which shows the difference between the number of 'decreasing' and 'increasing' words for each Sonnet.

Figure 3

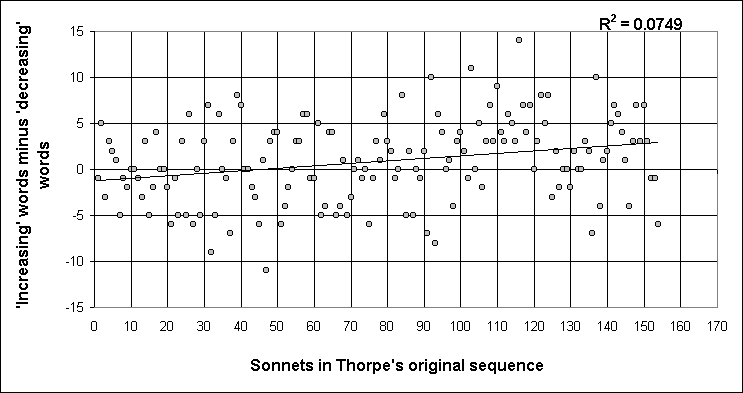
With an average of only about 114 words per sonnet there is bound to be a fairly wide variation, but the trend is clear nevertheless, even without seeing the linear trendline and its R² value of .0749. Compare the numbers above and below the zero line in each half.

There would obviously be some disagreement as to where breaks should occur, but it is possible to identify a few points in the sequence where the overall theme seems to undergo a change. One very rough way of splitting them might be as follows, to which is added the average score of each group, found by dividing its 'decreasing' total by its 'increasing'.

As can be easily seen, all follow the expected sequence except the first 17, which look as though they might have been written some time nearer the middle of the sequence and the Dark Lady group, which might have been a little earlier, but not much.

There can be little doubt that the use of function words does provide us with important evidence related to the overall sequence of Shake-speare's Sonnets. Whilst there are probably other sonnets in the wrong place, it would certainly seem likely that Thorpe's sequence is nearer to the order in which the Sonnets were actually written than any general attempt to impose a more 'logical' order upon them has been.

The revised sequences proposed by 19 different authors and editors (most of the earlier ones obtained from Hyder Edward Rollins 1944 'New Varorium' edition of The Sonnets) have therefore been examined to see how far each one 'matches' the sequence which would be suggested by this function word ratio. The relevant works were as follows.

By reordering the sonnets according to the scores in Figure 3, it is possible to say what the most probable sonnet sequence is, whilst accepting that this is certainly not the actual original sequence. I shall call this the 'stylometrically determined sequence' (the SDS). As the following table shows, using Spearman's rank order coefficient, only one of the 19 sequences is nearer to this SDS than Thorpe's is, and the further each one is from Thorpe's original sequence, the more it also tends to depart from the SDS. This is displayed as Figure 4.

Figure 4

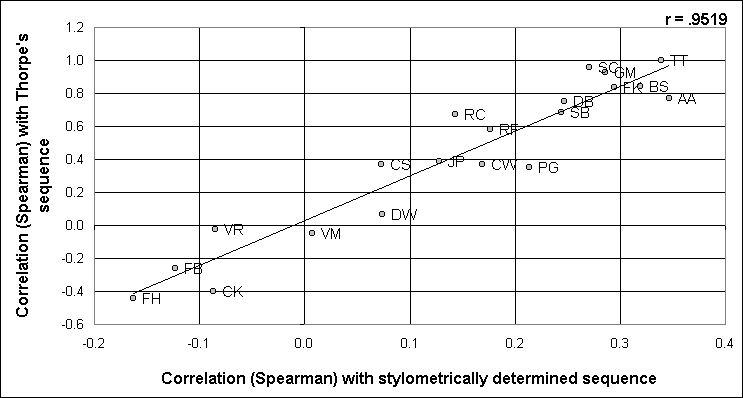
Picking numbers at random would therefore have a greater chance of being correct than those negatively correlated with the SDS.

The correlation between the two sets of figures (r = .9519) is clearly illustrated in Figure 4.

We have seen that Shakespeare's use of certain function words decreased over the course of his career, while the use of some others increased. Plotting the ratio of one set of such words to the other indicated a highly significant trend over time.

Using the same ratio in the case of The Sonnets, we found a similar trend occurred when plotted against the sequence in which they were originally printed. The trend was also more pronounced in this case than in that of all except one of 19 other suggested sequences.

In the case of Shakespeare's other works, the trend was chronologically based. We may therefore state with a high level of confidence that this applies in the case of The Sonnets too. In other words, that the period over which they were written probably covered several years, and that Thomas Thorpe's original sequence is to a large extent the one in which they were originally written.

© Peter Farey, 1998